Air Quality Assessment
Develop statistical methods to measure the effectiveness of the air pollution mitigation strategies based on objective air quality measures that remove the meteorological confounding.
| 空气质量评估平台 |
Reports
Publications
| 1 | Liang, X., T. Zou, B. Guo, S. Li, H. Zhang, S. Zhang, H. Huang and S. X. Chen. (2015). Assessing Beijing's PM2.5 Pollution: Severity, Weather Impact, APEC and Winter Heating, Proceedings of the Royal Society A, 471, 20150257. | [pdf] |
|---|---|---|
| 2 | Liang, X., Li, S., Zhang, SY, Huang, H. and S.X. Chen (2016). PM2.5 Data Reliability, Consistency and Air Quality Assessment in Five Chinese Cities, Journal of Geophysical Research:Atmosphere, 121, 10,220_10,236. | [pdf] |
| 3 | Zhang S, Guo B, Dong A, He J, Xu Z, Chen SX. 2017 Cautionary tales on air-quality improvement in Beijing. Proc. R. Soc. A 20170457. | [pdf] |
| 4 | Lei Chen, Bin Guo, Jiasheng Huang, Hengfang Wang, Shuyi Zhang and Song Xi Chen (2018). Assessing Air-Quality in Beijing-Tianjin-Hebei Region: the Method and Mixed Tales of PM2.5 and O3. Atmospheric Environment 193 (2018) 290–301. | [pdf] |
| 5 | Li, HB, Wu, JW., Wang, AX, Li, X, Chen, SX, Wang, TQ, Amsalu, E., Gao, Q., Luo, YX, Yang, XH., Wang, W, Guo, J., Guo, YM, Guo, XH. (2018). Effects of ambient carbon monoxide on daily hospitalizations for cardiovascular disease: a time-stratified case-crossover study of 460,938 cases in Beijing, China from 2013 to 2017, ENVIRONMENTAL HEALTH, 17:82. | [pdf] |
| 6 | Ziping Xu, Song Xi Chen, Xiaoqing Wu (2020) Meteorological Change and Impacts on Air Pollution Results from North China, Journal of Geophysics Research-Atmosphere, 125 (16), e2020JD032423. | [pdf] |
| 7 | 张澍一,陈松蹊,郭斌,王恒放,林伟(2020) 气象调整下的区域空气质量评估(Regional Air-Quality Assessment That Adjusts for Meteorological Confounding),中国科学:数学(Scientia Sinica Mathematica), 50,527~558. [English Version pdf] | [pdf] |
| 8 | Yating Wan, Minya Xu, Hui Huang and Song Xi Chen(2020) A spatio-temporal model for the analysis and prediction of fine particulate matter concentration in Beijing, Enviromentrics, e2648 | [pdf] |
| 9 | Wu, H., Zheng, X., Zhu, J., Lin, W., Zheng, H., Chen, X., Wang, W., Wang, Z., and S. X. Chen (2020). Improving PM2.5 forecasts in China suing an initial error transport model, Environmental Science and Technology, 54(17), 10493-10501. | [pdf] |
| 10 | Zheng, X-Y., Guo, B., He, J. and Chen, S.X. (2020) Effects of corona virus disease-19 control measures on air quality in North China (Invited paper), Environmetrics. 2021, e2673 | [pdf] |
| 11 | Li, S., Liu, R., Wang, S., & Chen, S. X. (2021). Radiative effects of particular matters on ozone pollution in six North China cities. Journal of Geophysical Research: Atmospheres, 126, e2021JD035963 | [pdf] |
| 12 | 吴煌坚,林伟,孔磊,唐晓,王威,王自发,陈松蹊 (2021) 一种基于集合最优插值的排放源快速反演方法, 《气候与环境研究》, 第26卷第2期。 | [pdf] |
| 13 | Yuru Zhu, Yinshuang Liang, Song Xi Chen(2021) Assessing Local Emission for Air Pollution via Data Experiments, Atmospheric Environment, 252, 118323. | [pdf] |
| 14 | Yaxuan Huang, Bin Guo, Haoxuan Sun, Huijie Liu and Song Xi Chen(2021) Relative Importance of Meteorological Variables on Air Quality and Role of Boundary Layer Height, Atmospheric Environment 267 (2021) 118737. | [pdf] |
| 15 | Tong, P. F., Chen, S. X., & Tang, C.Y. (2022). Detecting and evaluating dust-events in North China with ground air quality data. Earth and Space Science, 9, e2021EA001849 | [pdf] |
| 16 | Luo, S., Zhu, Y., & Chen, S. X. (2022). Episode based air quality assessment. Atmospheric Environment, 285, 119242. | [pdf] |
| 17 | Ying Zhang, Song Xi Chen, Le Bao(2023). Air pollution estimation under air stagnation—A case study of Beijing. Environmetrics, 34(6), e2819. https://doi.org/10.1002/env.2819 | [pdf] |
| 18 | Zheng, X-Y. and Chen, S.X. (2024) Dynamic synthetic control method for evaluating treatment effects in auto-regressive processes. Journal Of The Royal Statistical Society Series B-statistical Methodology, 86(1): 155-176. | [pdf] |
| 19 | Su, W., Wang, B., Chen, H. et al. (2024)A new global carbon flux estimation methodology by assimilation of both in situ and satellite CO2 observations. npj Clim Atmos Sci 7, 287 (2024). https://doi.org/10.1038/s41612-024-00824-w | [pdf] |
| 20 | Chen, HY, Chen SX and JK Qiu (2025) Comments on 'Consistent climate fingerprinting' by McKitrick (2025).Climate Dynamics 63, 261 (2025). | [pdf] |
High Dimensional Statistical Inference
Development methods applicable to a new norm of data: the dimension of the data is much larger than the number of sample points as commonly encountered in genetic and bio-medical studies, brain imaging and social and economic analyses.
Publications
| 1 | Chen, S. X., L. Peng and Y-L, Qin (2009). Effects of Data Dimension on Empirical Likelihood, Biometrika, 96, 711_722. | [pdf] |
|---|---|---|
| 2 | Chen, S.X., Zhang, L-X. and P-S Zhong (2010). Testing high dimensional covariance matrices. Journal of the American Statistical Association, 105, 810-819. | [pdf] Code |
| 3 | Chen, S. X. and Y. L. Qin (2010). A two sample test for high dimensional data with application to gene-set testing, The Annals of Statistics, 38, 808-835. | [pdf] Code |
| 4 | P-S Zhong and S. X. Chen (2011). Tests for High Dimensional Regression Coefficients with Factorial Designs. Journal of the American Statistical Association, 106, 260-274. | [pdf] Code |
| 5 | Li, J. and S. X. Chen (2012). Two Sample Tests for High Dimensional Covariance Matrices, The Annals of Statistics, 40, 908-940. | [pdf] Code |
| 6 | Qiu, Y-M and Chen, S. X. (2012). Test for Bandedness of High Dimensional Covariance Matrices with Bandwidth Estimation, TheAnnals of Statistics, 40, 1285-1314. | [pdf] Code |
| 7 | Zhong, P-S, Chen, S. X. and Xu M. (2013). Tests alternative to higher criticism for high dimensional means under sparsity and column-wise dependence, Annals of Statistics, 41, 2820-2851. | [pdf] Code |
| 8 | Qiu, Y-M and Chen, S.X. (2015) Band Width Selection for High Dimensional Covariance Matrix Estimation. Journal of the American Statistical Association, 110, 1160-1174. | [pdf] Code |
| 9 | Chang, J-Y, Chen, S.X. and X. Chen (2015). High Dimensional Generalized Empirical Likelihood for Moment Restrictions with Dependent Data. Journal of Econometrics, 185, 283-304. | [pdf] |
| 10 | Guo, B. and S.X.Chen (2016). Tests for High Dimensional Generalized Linear Models. Journal of the Royal Statistical Society, Series B. 78, 1079–1102. | [pdf] Code |
| 11 | Peng, LH, S.X. Chen and W, Zhou (2016) More Powerful Tests for Sparse High-Dimensional Covariances Matrices, Journal of Multivariate Analysis, 149, 124-143. | [pdf] Code |
| 12 | He, J. and S. X. Chen (2016) Testing Super-Diagonal Structure in High Dimensional Covariance Matrices, Journal of Econometrics, 194, 283-297 | [pdf] Code |
| 13 | Jing He and Song Xi Chen (2018). High-Dimensional Two-Sample Covariance Matrix Testing via Super-Diagonals. Statistica Sinica 28 (2018), 2671-2696 | [pdf] |
| 14 | Qiu, Y., Chen, S.X. and Nettleton, D.(2018)Detecting Rare and Faint Signals via Thresholding Maximum Likelihood Estimators, Annals of Statistics, 46, 895-923. | [pdf] |
| 15 | S.X. Chen, J. Li and P.-S. Zhong (2019), Two-Sample and ANOVA Tests for High Dimensional Means, The Annals of Statistics, Vol. 47, No. 3, 1443-1474. | [pdf] Code |
| 16 | Mao, X., Chen, SX and Wong, R.(2019) Matrix Completion with Covariate Information, Journal of the American Statistical Association, 2019, VOL. 114, NO. 525, 198–210, Theory and Methods | [pdf] |
| 17 | Mao, X-J., Wong, R. K-W and Chen, S. X. (2021) Matrix Completion under Low-Rank Missing Mechanism, Statistica Sinica, 31 (2021), 2005-2030. | [pdf] |
| 18 | Chang, J-Y., Chen, S.X., Tang, C-Y. and Wu, T-T (2021) High-dimensional empirical likelihood inference, Biometrika, 108, 127-147. | [pdf] |
| 19 | Song Xi Chen, Bin Guo and Yumou Qiu(2023). “Testing and signal identification for two-sample high-dimensional covariances via multi-level thresholding.” Journal of Econometrics, 235(2), 1337-1354. | [pdf] |
| 20 | Chen, S.X., Qiu, Y.M. and S.Y. Zhang (2023) Sharp Optimality for High Dimensional Covariance Testing under Sparse Signals, The Annals of Statistics,51(5): 1921-1945. | [pdf] |
| 21 | Hao-Xuan Sun, Shouxia Wang, Xiaogu Zheng, Song Xi Chen(2024)High-dimensional Ensemble Kalman Filter with Localization, Inflation and Iterative Updates. Quarterly Journal of the Royal Meteorological Society, QJ-24-0005.R2 | [pdf] |
| 22 | Zhang, SY, S.X. Chen and Yumou Qiu (2025) Mean Tests For High-dimensional Time Series, Statistica Sinica 35, 171-201 | [pdf] |
| 23 | Song Xi Chen(2026) Statistical Signal Detection in High Dimension. Proceeding of International Meeting of Mathematicians, to appear. | [pdf] |

Empirical Likelihood
参数似然是传统统计学的核心方法, 极大似然估计和似然比检验是统计学的基本方法。参数似然具有两个标志性结果。一个是Wilks定理,即参数似然比具有渐进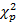 分布。另一个是以英国皇家院士Bartlett命名的巴特莱特调整。参数似然的局限是依赖于过强的模型设定。
分布。另一个是以英国皇家院士Bartlett命名的巴特莱特调整。参数似然的局限是依赖于过强的模型设定。
经验似然是由斯坦福大学Art Owen在1988年提出的,在比参数似然更弱的模型设定下构造似然函数的方法,英国皇家、美澳科学院院士Peter Hall曾指出:“经验似然是近年提出的非参数方法的有力竞争对手,会成为计算密集型统计方法的重要一员”。陈松蹊在几个重要框架下建立了经验似然的一阶Wilks定理和二阶巴特莱特调整,为经验似然成为基本的非参数统计方法贡献了关键性结果。
Publications
| 1 | Chen, S.X. and Hall, P. (1993). Smoothed empirical likelihood confidence intervals for quantiles. Ann. Of Statistics, 21,1166-1181. | [pdf] |
|---|---|---|
| 2 | Chen, S.X. (1993). On the coverage accuracy of empirical likelihood confidence regions for linear regression model. Annals of Institute of Statistical Mathematics, 45, 621-637. | [pdf] |
| 3 | Chen, S.X. (1994). Comparing empirical likelihood and bootstrap hypothesis tests. J. Mult. Anal, 51, 277-293. | [pdf] |
| 4 | Chen, S.X. (1994). Empirical likelihood confidence intervals for linear regression coefficients. J. Mult. Anal. 49, 24-40. | [pdf] |
| 5 | Chen, S.X. and Hall, P. (1994). On the calculation of standard error for quotation in confidence statements. Statistics and Probability Letters,19,147-151. | [pdf] |
| 6 | Chen, S.X. (1996). Empirical likelihood confidence intervals for nonparametric density estimation. Biometrika, 83, 329-341. | [pdf] |
| 7 | Chen, S.X. (1997). Empirical likelihood-based kernel density estimation. Aust. J. Statist. , 39,47-56 | [pdf] |
| 8 | Brown, B. M. and Chen, S. X. (1998). Combined Empirical Likelihood. Ann. Inst. Statist. Math, 50, 697-714. | [pdf] |
| 9 | Chen, S. X. and Qin, Yong Song (2000). Empirical Likelihood confidence interval for a local linear smoother. Biometrika, 87, 946-953. | [pdf] |
| 10 | Chen, S. X., Hardle, W. and Kleinow, T. (2002). An empirical likelihood goodness-of-fit test for diffusions. Applied quantitative finance, 259--281, Springer, Berlin. | |
| 11 | Chen, S. X. and Qin, Y-S. (2003). Coverage accuracy of confidence intervals in nonparametric regression. Acta Math. Appl. Sin. Engl. Ser.19,387--396. | [pdf] |
| 12 | Chen, S. X., D. H. Y. Leung and Qin, J. (2003). Information Recovery in a Study with Surrogate Endpoints. Journal of the American Statistical Association, 98,1052--1062. | [pdf] |
| 13 | Chen, S. X. and Qin, J. (2003). Empirical likelihood based confidence intervals for data with possible zero observations. Statistics and Probability Letters, 65, 29-37. | [pdf] |
| 14 | Chen, S. X., Haredle, W. and Li, M. (2003). An empirical likelihood goodness-of-fit test for time series. Journal of The Royal Statistical Society, Series B, 65, 663-678. | [pdf] |
| 15 | Chen, S. X and Cui, H-J. (2003). An extended empirical likelihood for generalized linear models. Statistica Sinica, 13, 69-81. | [pdf] |
| 16 | Cui, H-J and Chen, S.X. (2003).Empirical likelihood confidence regions for parameter in the errors-in-variables models, Journal of Multivariate Analysis, 84 (1), 101-115. | [pdf] |
| 17 | Chen, S.X. and H.-J., Cui (2006). On Bartlett Correction of Empirical Likelihood in the Presence of Nuisance Parameters, Biometrika, 93, 215-220. | [pdf] |
| 18 | Chen, S.X. and Qin, J. (2006). An Empirical likelihood Method in Mixture Models with Incomplete Classifications, Statistica Sinica,16, 1101-1115. | [pdf] |
| 19 | Chen, S.X. and J. Gao (2007). An Adaptive Empirical Likelihood Test For Time Series Models, paper, full report, Journal of Econometrics, 141, 950-972. | [pdf] |
| 20 | Chen, S.X. and H.-J., Cui (2007). On the second order properties of empirical likelihood with moment restrictions , Journal of Econometrics, 141, 492-516. | [pdf] |
| 21 | Chen, S. X., Leung, D. Y. H. and J. Qin (2008). Improving Semiparametric Estimation Using Surrogate Data. Journal of the Royal Statistical Society, Series B, 70, 803-823. | [pdf] |
| 22 | Chen, S.X., J. Gao and C. Y. Tang (2008). A Test for Model Specification of Diffusion Processes. The Annals of Statistics, 36, 167-198. | [pdf] |
| 23 | Chan, N-H, Chen, S.X., Peng, L. and C. L. Yu (2009). Empirical Likelihood Methods Based on Characteristic Functions with Applications to L'evy Processes. Journal of the American Statistical Association, 104, 1621-1630. | [pdf] |
| 24 | Chen, S. X. and I. Van Keilegom (2009). A review on empirical likelihood for regressions (with discussions), Test, 3, 415-447 . | [pdf] |
| 25 | Chen, S. X. and Van Keilegom, I. (2009). Empirical likelihood test for a class of regression models. Bernoulli, 15, 955-976. | [pdf] |
| 26 | Wang, D. and S.X. Chen (2009). Empirical Likelihood for Estimating Equation with Missing Values. The Annals of Statistics, 37, 490_517. | [pdf] |
| 27 | Wang, D. and Chen, S. X. (2009). Combining quantitative trait loci analyses and microarray data, an empirical likelihood approach. Computational Statistics and Data Analysis, 53, 1661_1673. | [pdf] |
| 28 | Chen, S.X. and Chiumin Wong (2009). Smoothed Block Empirical Likelihood for Quantiles of Weakly Dependent Processes, Statist Sinica, 19, 71-82. | [pdf] |
| 29 | Chen, S. X., L. Peng and Y-L, Qin (2009). Effects of Data Dimension on Empirical Likelihood, Biometrika, 96, 711_722. | [pdf] |
| 30 | Chen, S. X. and P-S Zhong (2010). ANOVA for longitudinal data with missing values. The Annals of Statistics, 38, 3630-3659. | [pdf] |
| 31 | Chen, S.X. and J. Gao (2011). Simultaneous Specification Test for the Mean and Variance Structures for Nonlinear Time Series regression. Econometric Theory, 27, 2011, 792_843. | [pdf] |
| 32 | Qiu, Y-M and Chen, S. X. (2012). Test for Bandedness of High Dimensional Covariance Matrices with Bandwidth Estimation, TheAnnals of Statistics, 40, 1285-1314. | [pdf] Code |
| 33 | Chang, J-Y, Chen, S.X. and X. Chen (2015). High Dimensional Generalized Empirical Likelihood for Moment Restrictions with Dependent Data. Journal of Econometrics, 185, 283-304. | [pdf] |
| 34 | Chang, J-Y., Chen, S.X., Tang, C-Y. and Wu, T-T (2021) High-dimensional empirical likelihood inference, Biometrika, 108, 127-147. | [pdf] |

Econometrics
Modeling and analyses of Chinese economic data and general econometric methods.
Publications
| 1 | Chen, S. X. and Tang, C. Y. (2005). Nonparametric Inference of Value at Risk for dependent Financial Returns. Journal of Financial Econometrics, 3, 227-255. | [pdf] |
|---|---|---|
| 2 | Chen, S.X. and H.-J., Cui (2007). On the second order properties of empirical likelihood with moment restrictions , Journal of Econometrics, 141, 492-516. | [pdf] |
| 3 | Chen, S.X. and J. Gao (2007). An Adaptive Empirical Likelihood Test For Time Series Models, paper, full report, Journal of Econometrics, 141, 950-972. | [pdf] |
| 4 | Chen, S.X: (2008). Nonparametric Estimation of Expected Shortfall. Journal of Financial Econometrics, 6, 87-107. | [pdf] |
| 5 | C. Y. Tang and S. X. Chen (2009). Parameter estimation and bias correction for diffusion processes. Journal of Econometrics, 149, 65-81. | [pdf] |
| 6 | Chen, S. X., Delaigle, A. and Hall, P. (2010). Nonparametric estimation for a class of levy processes, Journal of Econometrics, 157, 257-271. | [pdf] |
| 7 | J. Chang and S.X. Chen (2011). On the approximate maximum likelihood estimation for diffusion processes. The Annals of Statistics, 39, 2820-2851. | [pdf] |
| 8 | Chen, S.X. and J. Gao (2011). Simultaneous Specification Test for the Mean and Variance Structures for Nonlinear Time Series regression. Econometric Theory, 27, 2011, 792_843. | [pdf] |
| 9 | Chen, S.X. and Z. Xu (2013). On smoothing estimation for seasonal time series with long cycles, Statistics and Its Interface, 6, 435-447. | [pdf] |
| 10 | Chen, S.X. and Z. Xu (2014). On Implied Volatility for Options - Some Reasons to Smile and More to Correct. Journal of Econometrics, 179, 1-15. | [pdf] |
| 11 | Chang, J-Y, Chen, S.X. and X. Chen (2015). High Dimensional Generalized Empirical Likelihood for Moment Restrictions with Dependent Data. Journal of Econometrics, 185, 283-304. | [pdf] |
| 12 | Wang, Y., Tu, Y-D and S. X. Chen (2016) Improving inflation prediction with the quantity theory. Economics Letters, 149, 112-115. | [pdf] |
| 13 | He, J. and S. X. Chen (2016) Testing Super-Diagonal Structure in High Dimensional Covariance Matrices, Journal of Econometrics, 194, 283-297 | [pdf] Code |
| 14 | Chen, S.X., Lei, L.-H. and Tu, Y-D (2016). Functional Coefficient Moving Average Models with applications to forecasting Chinese CPI, Statistica Sinica, 26, 1649-1672. | [pdf] |
| 15 | Tao Zou & Song Xi Chen (2017) Enhancing Estimation for Interest Rate Diffusion Models With Bond Prices, Journal of Business & Economic Statistics, 35:3, 486-498 | [pdf] |
| 16 | 王振中,陈松蹊,涂云东(2023)中国居民消费价格指数的动态结构研究及中美量化比较,数理统计与管理,42:109-126. | [pdf] |
COVID-19
The COVID-19 pandemic, also known as the coronavirus pandemic, have caused more than 179.5 million confirmed cases and 3.9 million deaths by June 22, 2021, making it one of the deadliest pandemics in history.
On Jan 23, 2020 --- The day when the 76-day lockdown began in Wuhan, Professor Chen organized a team aiming at fighting against this global pandemic. Since then, Chen’s group have contributed quite a lot in giving advice on controlling the outbreak of the pandemic via statistical data analysis. By May 5th, the group had released 5 domestic and 8 international COVID-19 briefing reports, which offered much insight to the government on policy-making.
International Reports
Domestic Reports
Publications
| 1 | Haoxuan Sun, Yumou Qiu, Han Yan, Yaxuan Huang, Yuru Zhu, Jia Gu and Song Xi Chen(2020) Tracking Reproductivity of COVID-19 Epidemic in China with Varying Coefficient SIR Model (with discussion), Journal of Data Science 18 (3), 455–472. | [pdf] |
|---|---|---|
| 2 | Zheng, X-Y., Guo, B., He, J. and Chen, S.X. (2020) Effects of corona virus disease-19 control measures on air quality in North China (Invited paper), Environmetrics. 2021, e2673 | [pdf] |
| 3 | Jia Gu, Han Yan, Yaxuan Huang, Yuru Zhu, Haoxuan Sun, Yumou Qiu and SongXi Chen(2020). Comparing Containment Measures among Nations by Epidemiological Effects of COVID-19. National Science Review, 7: 1847–1851. doi: 10.1093/nsr/nwaa243. | [pdf] |
| 4 | Han Yan, Yuru Zhu, Jia Gu, Yaxuan Huang, Haoxuan Sun, Xinyu Zhang, Yuqing Wang, Yumou Qiu, Song Xi Chen(2021) Better Strategies for Containing COVID-19 Pandemic–A Study of 25 Countries via a vSIADR Model, Proceedings of the Royal Society A, 476: 20200440. | [pdf] |
| 5 | Chen, S.X. and Zheng, XY (2021) Discussion on ``The Timing and Effectiveness of Implementing Mild Interventions of COVID-19 in Large Industrial Regions via a Synthetic Control Method", Statistics and Its Interface, 14 (2021), 1, 23-24. | |
| 6 | 顾嘉 陈松蹊, 董倩, 邱宇谋 (2021)基于vSEIdRm模型的人口迁移以及离汉交通管控对新冠肺炎疫情发展的影响分析,统计研究,Vol.38, No.9 | [pdf] |
| 7 | Yuru Zhu, Jia Gu, Yumou Qiu, And Song Xi Chen (2023) Estimating COVID-19 Vaccine Protection Rates Via Dynamic Epidemiological Models–A Study Of Ten Countries. The Annals of Applied Statistics,17(4):3324–3348. | [pdf] |
| 8 | Yuru Zhu, Jia Gu, Yumou Qiu, and Song Xi Chen(2023) Real-World COVID-19 Vaccine Protection Rates against Infection in the Delta and Omicron Eras. Research. 2023:6;0099. DOI:10.34133/research.0099 | [pdf] |
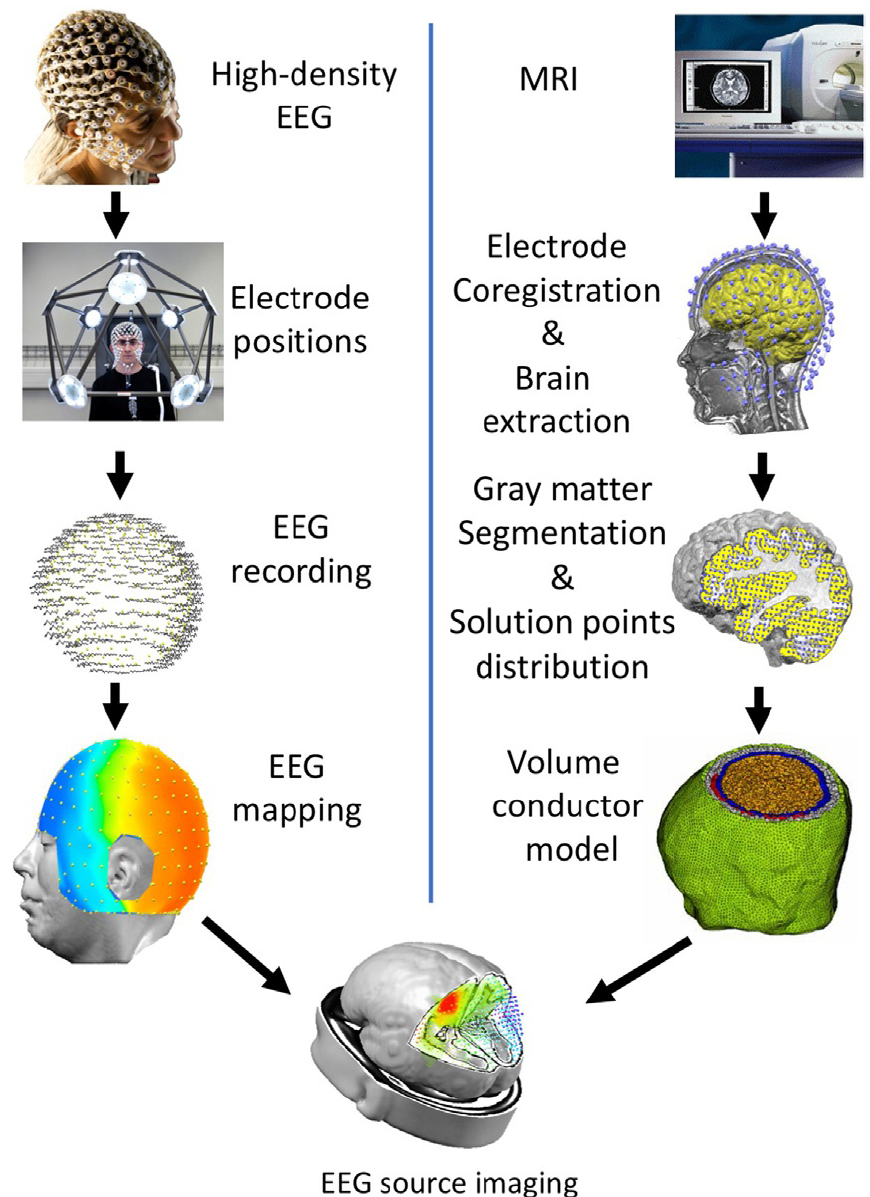
Neural Science
Analyzing EEG, MRI and CT data with statistical methods and deep learning techniques to tackle the key scientific challenges in diagnosing and treating major brain diseases.
Publications
| 1 | Tong, P.F., Zhan, H.X. and Chen, S.X. (2024) Ensembled Seizure Detection based on Small Training Samples, IEEE Transaction on Signal Processing, 72: 1-14.DOI:10.1109/TSP.2023.3333546 | [pdf] |
|---|---|---|
| 2 | Pei Feng Tong, Bosi Dong, Xiangdong Zeng, Lei Chen, Song Xi Chen. (2024) Detection of interictal epileptiform discharges using transformer based deep neural network for patients with self-limited epilepsy with centrotemporal spikes, Biomedical Signal Processing and Control, Volume 101, March 2025, 107238 | [pdf] |
| 3 | Pei Feng Tong, Haoran Yang, Xinru Ding, Yuchuan Ding, Xiaokun Geng, Shan An, Guoxin Wang, and Song Xi Chen.(2025) Debiased Estimation and Inference for Spatial–Temporal EEG/MEG Source Imaging. IEEE TRANSACTIONS ON MEDICAL IMAGING, VOL. 44, NO. 3 | [pdf] |